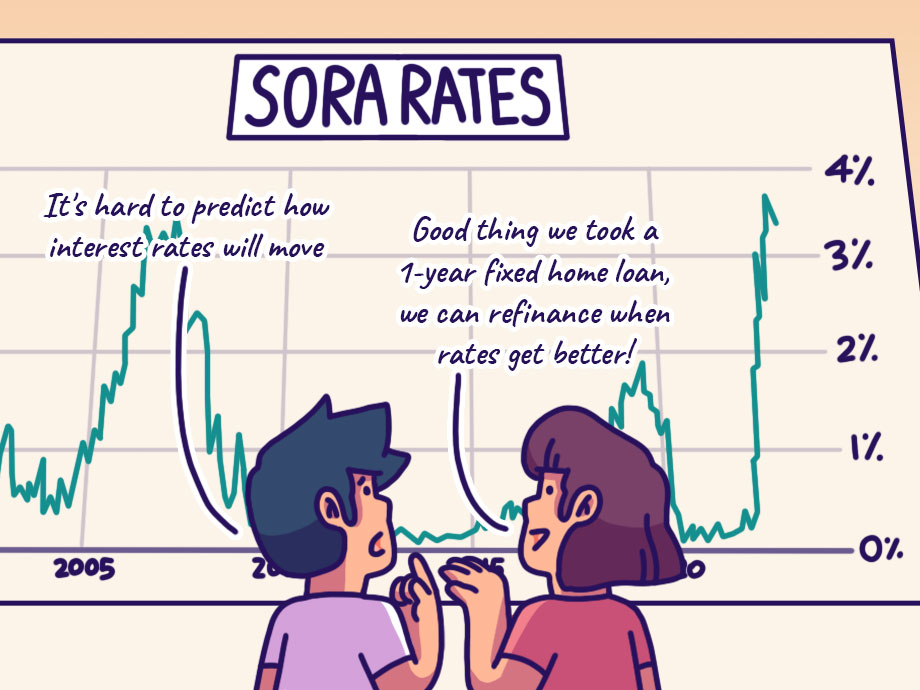
Financial Planning | Managing Debt | Personal Finance | Article
Making Sense of Effective Interest Rates
by YuanDuan | 1 Aug 2019 | 4 mins read
Any respectable Singaporean will obsess over finding the best deals and hunting for the lowest prices.
So, it should be no different when we consider taking a loan, borrowing at the lowest interest rates to get the best value.
But if you have been loan-hunting, you will have come across two interest rates displayed on the same loan. Nominal rates are the rate you see prominently displayed, screaming “LOWEST RATES IN TOWN”.
The more interesting rate is called the Effective Interest Rate (EIR), and this rate is always higher than the nominal rate.
So, what’s this EIR?
In Singapore, lenders are legally required to display EIRs, providing a transparent way for borrowers to evaluate borrowing costs.
Great, so how do we use it? Do we simply sign up for the loan that offers the lowest EIR?
As with most things in life, yes and no.
Why are there two interest rates?
Here is a nominal 2% interest rate in action.
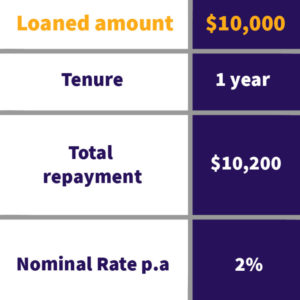
In this example, you pay $200 in interest – 2% of $10,000 – nothing surprising here.
But EIR takes other factors into consideration to provide a fuller picture of a loan’s costs.
EIR takes into account processing fees
EIR considers the admin and processing fees incurred when you sign up for a loan.
If we use the same $10,000 example, but tossing in a fee of $500. This means the $10,000 loan is now only “worth” $9,500.
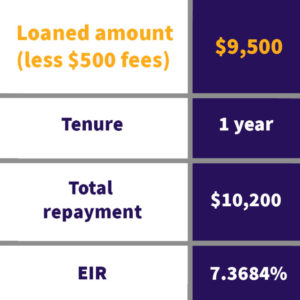
Because of the fees, the amount loaned is effectively reduced. Hence, the EIR is higher.
EIR also changes according to the repayment period
EIR also accounts for how interest is charged. For example, some loans might have their interest rates applied and compounded on a quarterly basis. But in advertising, the 4 quarter’s rates are totalled to display a single annual interest rate.
Here’s how it can work
Loan A – 2% applied annually, at the end of the year.
Loan B – compounded 0.5% every quarter (total 2%).
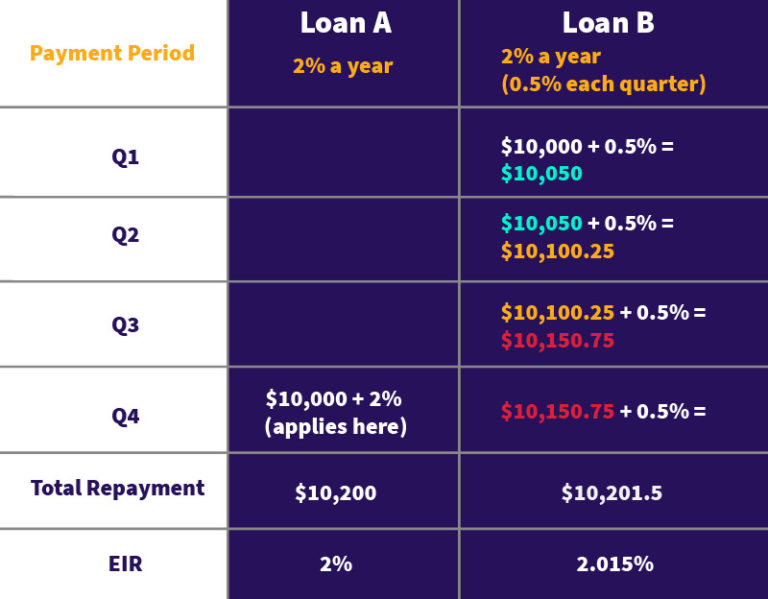
It’s a small difference, but it’s there.
Frequency of installments
How often a loan schedules its installments also affects EIR. Again, let’s compare between two 1 year, $10,000 loans with a nominal interest rate of 2%. But this time the difference is in their repayment schedules.
- Loan A
- $850 monthly installments
- Total of $10,200 repaid
- EIR 3.73%
- Loan B
- $2,550 quarterly installments
- Also a total of $10,200 repaid
- EIR 3.23%
This is perhaps the most confusing part about EIR, it’s the same repayment amount of $10,200, within the same time period.
But Loan A has the higher EIR. What gives?
This is because EIR takes into account how quickly you make start repaying the loan.
This makes sense because the quicker you have to repay, the less time you have to enjoy the money. Imagine walking out of a bank with a fat loan, but having to repay the first installment within two days, that sucks.
When using EIR is not a good idea
So far, it’s plain to see that taking the loan with the lowest EIR can be a great tool to help you select the cheapest loan.
But be careful when selecting a loan purely on the basis EIR. At the bigger picture, longer tenure loans will always have more interest charged – even with lower EIR – here is a simple example.
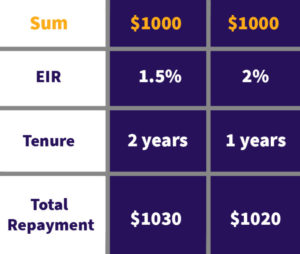
So as you can see, while useful, EIR can’t be the end-all in the loan selection process.
But if you read up to here, you might have gotten an inkling on how to use EIR effectively: Comparing loans with similar tenures to find the best value, and in this case, it’s certain that the lower the EIR the better.